domingo, 5 de octubre de 2008
OPINION ACERCA DE CURSO ESTADISTICA
el aula virtual bueno eso es una clase el la que nosotros estamos empezando ha conocer y que debemos explorarla para que en cualquier momento nosotros como futuros profesionales tengamos esa idea de que es una aula virtual.
bueno el curso de estadistica esta bastante bien prof. lo felicito que siga adelante con su labor.........
martes, 16 de septiembre de 2008
ESPERANZA MATEMATICAS
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética
Para una variable aleatoria discreta con valores posibles y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:

COMENTARIO:
LA ESPERANZA MATEMATICAS ES UN PROCESO QUE ESTUDIA Y QUE PERMITE COMPARAR DOS O MAS ELEMENTOS O ALTERNATIVAS QUE CONTIENE EL FENOMENO O ESTUDIO.
DIAGRAMA DE ARBOL
Ejemplos:
1.Un médico general clasifica a sus pacientes de acuerdo a: su sexo (masculino o femenino), tipo de sangre (A, B, AB u O) y en cuanto a la presión sanguínea (Normal, Alta o Baja). Mediante un diagrama de árbol diga en cuantas clasificaciones pueden
estar los pacientes de este médico?
N
Solución: A
A B
N
B A
B
M AB N
A
O B
A
N
F B A
B
AB
B
O A
B
COMENTARIO:
EL DIAGRAMA DE ARBOL TRATA DE RECOPILAR TODO ELEMENTO POSIBLE A DAR UN RESULTADO DEL PROCESO O ESTUDIO QUE SE ESTA REALIZANDO.
viernes, 12 de septiembre de 2008
COMBINACION Y PERMUTACION.
Es todo arreglo de elementos en donde no nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
PERMUTACIÓN:
Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
COMENTARIO:
COMBINACION MAS QUE TODO EN ESE PROCESO ES EL ARREGLO DE LOS ELEMENTOS NO IMPORTANDO EL ORDEN Y EN PERMUTACION EN ESTE PROSESO SI IMPORTA EL ORDEN Y LUGAR DE LOS ELEMENTOS.
sábado, 6 de septiembre de 2008
PROBABILIDAD.
EJEMPLO 1: sea X el número de caras obtenidas al lanzar 3 veces una moneda. Aquí los valores de X son x = 0, 1, 2, 3
Como se muestra en el ejemplo 1 estos valores son Numerables, y Finitos, ya que se nos da un numero de especifico de casos y solo nos pueden dar un numero especifico de resultados.
COMENTARIO:
LA PROBABILIDAD ESTUDIA, MIDE LA FRECUENCIA CON LA QUE APARECE UN DETERMINADO RESULTADO DE UN EXPERIMENTO QUE YA HA SIDO ESTUDIADO.
TEORIA DE CONTEO.
.- Consideraremos a W como el conjunto universal el cual posee todos los elementos posibles, así el conjunto A es un subconjunto de W si todos los elementos de A son elementos de W, y se denota:
A Ì W si para todo x ÎA, x Î W
.- Sean A y B dos conjuntos cuales quiera entonces:
la unión se define como: C = A È B = { x / xÎA o xÎB};
la intersección se define como: C = A Ç B = { x / xÎA y xÎB};
el complemento se define como: Ac = { x Î W / x Ï A },
El conjunto que no posee elementos se denomina conjunto vacío y se denota por Æ . (Notemos que A Ç Ac = Æ )
Diremos que A y B son disjuntos o mutuamente excluyente si: A Ç B = Æ.
Para resolver algunos problemas de probabilidades es necesario conocer el numero de elementos que posee cierto conjunto y el conjunto universal, denominado, en probabilidades, espacio muestral, es por ello que se debe saber como determinar el número de elementos de cualquier conjunto, tarea que puede ser algo complicado, sin embargo en algunos casos esto se puede realizar y por ello es que es importante el aprender a calcular este número.
COMENTARIO:
LA TEORIA DE CONTEO SE TRATA DE PROBLEMAS QUE ENTRETIENEN AL RELACIONAR DOS CONJUNTOS A LA HORA DE OPERARLOS EN UNA UNION O YA SEA EN UN INTERSECCION O DIFERENCIA EN LA CUAL PERMITE OBTENER DATOS QUE VAN RELACIONADOS CON LOS MISMOS.
jueves, 4 de septiembre de 2008
COMBINACIONES
Dado un conjunto de n elementos, se denomina combinaciones de tamaño r a todos los conjuntos que se pueden formar con r elementos tomados de entre los n elementos, de modo que cada conjunto difiera de los demás en por lo menos un elemento.
Siguiendo con el mismo ejemplo, si en un grupo de 10 personas se elegirá a 5 para tomarles una foto, ¿cuántos grupos de 5 pueden formarse, si el orden no importa?
Si el orden importara, habría A105 disposiciones diferentes. Pero en este caso no interesa el orden, así que si una de las posibilidades es Juan, María, Luis, Ana y Pedro, entonces la permutación Luis, Pedro, María, Ana y Juan corresponde a la misma combinación. Cada grupo de 5 personas puede ordenarse de 5! formas diferentes. Así, cada combinación corresponde a 5! permutaciones. Por lo tanto, el número de combinaciones satisface P5.(nº de combinaciones) = A105o sea que el número de combinaciones es igual a 10
A5
---- = 252
P5
En general, dados n objetos distintos, el número de combinaciones de tamaño r de estos objetos, con 0 <= r <= n, se denota Cnr y corresponde a
n
n Ar n!
Cr = ---- = --------
Pr r!(n-r)!
Ejemplo
Dadas las letras a, b, c existen 3 combinaciones de tamaño 2. 3 3!
C2 = ---- = 3
2!1!
Las 3 combinaciones son:a ba cb ca
COMENTARIO:
LAS COMBINACIONES DE UN CONJUNTO ES TODO AQUELO QEU EN UN CONJUNTO DADO SE RELACIONA LOS ELEMTOS DE ELLO SACANDOLOS DE PAR EN PAR.
martes, 2 de septiembre de 2008
DIFERENCIA
La diferencia se denota por: A - B que se lee: A diferencia B o A menos B. Se define la diferencia de dos conjuntos también como:
A - B = {x / x A y x B}
Mediante un diagrama de Venn - Euler:



COMENTARIO:
LA DIFERENCIA DE CONJUNTOS ES TODO AQUELLA DIFERENCIACION QUE SE DA ENTRE ELEMENTOS DE UN CONJUNTO DADO.
INTERSECCION DE CONJUNTOS.
A B = { x / x A y x B } y mediante un diagrama de Venn-Euler
COMENTARIO:
BASICEMENTE LA INTERSECCION DE CONJUNTOS FORMADOS POR ELEMENTOS QUE PERTENECEN A UN A Y AUN B SE DIFERENCIAN POR SER UNICOS ELEMENTOS EN UN CONJUNTO.
sábado, 30 de agosto de 2008
UNION DE CONJUNTOS
La unión de los conjuntos A y B es el conjunto formado por todos los elementos que pertenecen a A o a B o a ambos. Se denota: A U B. La unión de conjuntos se define como:
A U B = {x / x A o x B}
En forma gráfica



COMENTARIO:
LA UNION DE CONJUNTO MAS QUE TODO ES LA UNION DE DOS O MAS CONJUNTOS POR EL ELEMENTO QUE PERTENECE.
jueves, 28 de agosto de 2008
TEORIA DE CONJUNTOS.
El concepto de conjunto es intuitivo y se podría definir como una "colección de objetos"; así, se puede hablar de un conjunto de personas, ciudades, lapiceros o del conjunto de objetos que hay en un momento dado encima de una mesa. Un conjunto está bien definido si se sabe si un determinado elemento pertenece o no al conjunto. El conjunto de los bolígrafos azules está bien definido, porque a la vista de un bolígrafo se puede saber si es azul o no. El conjunto de las personas altas no está bien definido, porque a la vista de una persona, no siempre se podrá decir si es alta o no, o puede haber distintas personas, que opinen si esa persona es alta o no lo es. En el siglo XIX, según Frege, los elementos de un conjunto se definían sólo por tal o cual propiedad. Actualmente la teoría de conjuntos está bien definida por el sistema ZFC. Sin embargo, sigue siendo célebre la definición que publicó Cantor
Usualmente los conjuntos se representan con una letra mayúscula: A, B, K,...
Llamaremos elemento, a cada uno de los objetos que forman parte de un conjunto, estos elementos tienen carácter individual, tienen cualidades que nos permiten diferenciarlos, y cada uno de ellos es único, no habiendo elementos duplicados o repetidos. Los representaremos con una letra minúscula: a, b, k,...
De esta manera, si es un conjunto, y todos sus elementos, es común escribir:

para definir a tal conjunto . Esta notación empleada para definir al conjunto se llama notación por extensión
Para representar que un elemento pertenece a un conjunto A, escribimos (léase "x en A", "x pertenece a A" o bien "x es un elemento de A"). La negación de se escribe (léase no pertenece a ).
El conjunto universal, que siempre representaremos con la letra U (u mayúscula), es el conjunto de todas las cosas sobre las que estemos tratando. Así, si hablamos de números enteros entonces U es el conjunto de los números enteros, si hablamos de ciudades, U es el conjunto de todas las ciudades, este conjunto universal puede mencionarse explícitamente, o en la mayoría de los casos se da por supuesto dado el contexto que estemos tratando, pero siempre es necesario demostrar la existencia de dicho conjunto previamente.
Existe además, un único conjunto que no tiene elementos al que se le llama conjunto vacío y que se denota por . Es decir
La característica importante de este conjunto es que satisface todos los elementos posibles no están contenidos en él, es decir
.
Por otro lado, si todos los elementos de un conjunto A satisfacen alguna propiedad, misma que pueda ser expresada como una proposición , con la indeterminada , usamos la notación por comprensión, y se puede definir:
Lo anterior se lee "A es el conjunto de elementos x, que cumplen la propiedad p(x)". El símbolo ":" se lee "que cumplen la propiedad" o "tales que"; este símbolo puede ser remplazado por una barra .
Por ejemplo, el conjunto puede definirse por:
donde el símbolo representa al conjunto de los números naturales.
El uso de algún conjunto es muy importante, ya que de no hacerlo se podría caer en contradicciones como ejemplo:

COMENTARIO:
LA TEORIA DE CONJUNTOS BASICAMENTE ES LA COLECCION DE OBJETOS QUE SE OBTIENE AL ESTUDIAR UN CONJUNTO DE PEROSNAS, COSAS, CIUDADES, U OTRAS COSAS.
SUB CONJUNTOS
A es un subconjunto de B;
B es un superconjunto de A;
Todo conjunto A es un subconjunto de sí mismo. Cualquier subconjunto de A que no sea igual a A se denomina propio (cuando puede ser igual a A se denomina impropio). Si A es un subconjunto propio de B, escribimos:
De manera análoga si B es un superconjunto propio de A, escribimos:
El conjunto vacío, denotado como:
es un subconjunto de cualquier conjunto. Además el conjunto vacío es siempre un subconjunto propio, excepto de sí mismo
Proposición 1: Dados tres conjuntos A, B y C, si A es subconjunto de B y B es subconjunto de C, entonces A es subconjunto de C.
Proposición 2: Dos conjuntos A y B son iguales si y sólo si A es subconjunto de B y B es subconjunto de A.
Proposición 3: Para todo conjunto A, el conjunto vacío es un subconjunto de A.
Demostración: Dado cualquier conjunto A, queremos demostrar que {} es un subconjunto de A. Esto supone mostrar que todos los elementos de {} son elementos de A. Sin embargo, por definición, {} no tiene ningún elemento.
Para el matemático experimentado, la inferencia "{} no tiene elementos, así que todos los elementos de {} son elementos de A" es inmediata, pero puede ser más problemática para el principiante. Después de todo, como {} no tiene elementos, ¿cómo pueden "esos elementos" pertenecer a otro conjunto? Se puede razonar esto por contraposición. Para probar que {} no es un subconjunto de A, tendríamos que encontrar un elemento de {} que no esté en A. Como {} no tiene elementos, esto es imposible y por tanto {} es un subconjunto de A.ejmplo.


comentario:
Los subconjuntos basicamente representa el enlace de un A a un B y esto hace de que el subconjunto sean elementales y esto hace de que esten en el mismo circulo del elemento principal.
miércoles, 20 de agosto de 2008
MAPA CONCEPTUAL.
Aprendizaje Activo
Cuando se realiza un mapa conceptual, se obliga al estudiante a relacionarse , a jugar con los conceptos, a que se empape con el contenido. No es una simple memorización; se debe prestar atención a la relación entre los conceptos. Es un proceso activo.
Usos
El mapa conceptual puede tener varios propósitos:
generar ideas (lluvia de ideas [brain storming], etc.);
diseñar una estructura compleja (textos largos, hipermedia, páginas web grandes, etc.);
comunicar ideas complejas;
contribuir al aprendizaje integrando explícitamente conocimientos nuevos y antiguos;
evaluar la comprensión o diagnosticar la incomprensión;
explorar el conocimiento previo y los errores de concepto;
fomentar el aprendizaje significativo para mejorar el éxito de los estudiantes;
medir la comprensión de conceptos.
clasificar de forma similar a las palabras las cuales se encuentran en las diferentes temáticas que se puedan utilizar en el tema dado.
Cómo construir un mapa conceptual
Seleccionar
Agrupar
Ordenar
Representar
Conectar
Comprobar
Reflexionar
EJEMPLO:

comentario:
Los mapas conceptuales dan a entender ideas principales de un tema a desarrollar y que es mas eficiente para el manejo de temas muy amplios.
lunes, 21 de julio de 2008
CLASES DE TENDENCIA (cosntante y estocastica)
Es un concepto matemático que sirve para caracterizar y estudiar todo tipo fenómenos aleatorios (estocásticos) que evolucionan, generalmente, con el tiempo
Un proceso estocástico es una sucesión de variables aleatorias indexadas por una variable (continua o discreta), generalmente, el tiempo. Cada una de las variables aleatorias del proceso tiene su propia función de distribución de probabilidad y, entre ellas, pueden estar correlacionadas o no.
Cada variable o conjunto de variables sometidas a influencias o impactos aleatorios constituye un proceso estocástico.
Un proceso estocástico se puede definir equivalentemente de dos formas diferentes:
Como un conjunto de realizaciones temporales y un índice aleatorio que selecciona una de ellas.
Como un conjunto de variables aleatorias indexadas por un índice , dado que , con .
puede ser continuo si es un intervalo (el número de sus valores es ilimitado) o discreto si es numerable (solamente puede asumir determinados valores).
sábado, 19 de julio de 2008
CLASIFICACION DE SERIES TEMPORALES
1)una serie estacionaria si la media y la variabilidad se mantienen constantes a lo largo del tiempo.
2)es aquella en la que ni las autocorrelaciones dependen del tiempo,una vez estabilizada la serie mediante las trasnformaciones adecuadas, se procede a estudiar la presencia de regularidad en la serie para identificar un posible modelo matematico.
3) con las seires estacionarias podemos obtener predicciones facilmente , como la media es constante, podemos estimar con todos los datos y utilizando este valor, para predecir nuevas observaciones.

el vínculo entre los conceptos de cointegración y de modelos de mecanismo
de corrección del error, demostrando que las variables cointegradas
siempre pueden representarse en términos de dichos modelos
y viceversa
miércoles, 16 de julio de 2008
GRAFICAS DE SERIES DE TIEMPO/SERIES TEMPORALES
SERIES DE TIEMPO/SERIES TEMPORALES
En una serie de tiempo las observaciones no se deben ordenar de mayor a menor debidoa que se perderia el grueso de la informacion debido a que nos intersea detectar como se mueve la variable en el tiempo es muy importante respetar la secuencia temporal de las observaciones.
2)Una serie de tiempo o serie temporal es una colección de observaciones tomadas a lo largo del tiempo cuyo objetivo principal es describir, explicar, predecir y controlar algún proceso. Las observaciones están ordenadas respecto al tiempo y sucesivas observaciones son generalmente dependientes. De hecho esta dependencia entre las observaciones jugará un papel importante en el análisis de la serie.
3)una serie temporal es una secuencia de puntos de datos, medidos típicamente a intervalos de tiempo sucesivos , y espaciados (con frecuencia) de forma uniforme. El análisis de series temporales comprende métodos que ayudan a interpretar este tipo de datos, extrayendo información representativa, tanto referente a los orígenes o relaciones subyacentes como a la posibilidad de extrapolar y predecir su comportamiento futuro.
Representacion de una Serie Temporal
Par realizar la reprsenyacion de una serie ytemporal se debe realizae mediante una gráfica de disprsión x-y como se muestra en la fig.1

COMENTARIO:
ES EL ESTUDIO DE MEDIDAS DE UNA DETERMINADA VARIABLE DE UN FENOMENO PARA LA LOCALIZACION DE SU ESTACIONALIDAD O TENDENCIA EN EL TIEMPO.
sábado, 12 de julio de 2008
REGRESION CUADRATICA:
De nuevo hacemos una definición de la función de error, y encontramos los valores de los parámetros que la minimizan, tomando derivadas parciales de la función por cada parámetro que haya:
Regresión Cuadrática : y = A + Bx +Cx2
COMENTARIO:
LA REGRESION CUADRATICA PRACTICMENTE SE USA CUANDO LOS DATOS ESTAN MUY DISPERSOS EN FORMA DE PARABOLA EN DICHA ECUACION DEL PROBLEMA SE UTILIZA FORMULAS PARA LLEGAR A PODER DETERMINAR EL RESULATO DEL FENOMENO QUE SE ESTE ESTUDIANDO.
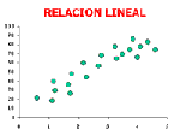
REGRESION LINEAL
El término regresión se utilizó por primera vez en el estudio de variables antropométricas: al comparar la estatura de padres e hijos, resultó que los hijos cuyos padres tenían una estatura muy superior al valor medio tendían a igualarse a éste, mientras que aquellos cuyos padres eran muy bajos tendían a reducir su diferencia respecto a la estatura media; es decir, "regresaban" al promedio.[4] La constatación empírica de esta propiedad se vio reforzada más tarde con la justificación teórica de ese fenómeno.
El término lineal se emplea para distinguirlo del resto de técnicas de regresión, que emplean modelos basados en cualquier clase de función matemática. Los modelos lineales son una explicación simplificada de la realidad, mucho más ágil y con un soporte teórico por parte de la matemática y la estadística mucho más extenso.
El modelo lineal relaciona la variable dependiente Y con K variables explicativas Xk (k = 1,...K), o cualquier transformación de éstas, que generan un hiperplano de parámetros βk desconocidos:


La regresión lineales un método de análisis de los datos de la realidad de un fenomelo que sirve para poner en evidencia las relaciones que existen entre diversas variables de su taryectoria en el tiempo.
lunes, 7 de julio de 2008
CORRELACION.
la influencia que pueda tener una sobre la otra.
Cuando dos variables están correlacionadas (altamente correlacionadas), una variable puede dar información sobre la otra.Si la información de una variable da información exacta sobre la otra, decimos que hay una Relación o dependencia funcional.Un ejemplo de lo anterior es la relación que existe entre el tiempo de usar el teléfono y el costo.Hablamos de Correlación DIRECTA, cuando al aumentar x, aumenta y. Hablamos de Correlación INVERSA, cuando al aumentar x, disminuye y. Hablamos de Correlación Nula, cuando no hay relación entre x e y.Ojo que la correlación se puede detectar, cualitativamente en un gráfico, en una nuve de puntos que relacionen las dos variables. Veamos algunos ejemplos:
La Correlación Lineal se mide utilzando el coeficiente de corelacion:
r cercano a -1, indica Correlación Lineal Negativa.
r cercano a 0, indica Correlación
1) Perfecta 1) R = 1
2) Excelente 2) R = 0.9 < = R < r =" 0.8" r =" 0.5">DISTRIBUCIÒN DIVARIANTE
DEFINICIÒN :
La correlación, método por el cual se relacionan dos variables se pude graficar con un diagrama de dispersión de puntos, a la cual muchos autores le llaman nubes de puntos, encuadrado dentro de un gráfico de coordenadas X Y en la cual se pude trazar una recta y cuyos puntos mas cercanos de una recta hablaran de una correlación mas fuerte, ha esta recta se le denomina recta de regresión, que puede ser positiva o negativa, la primera contundencia a aumentar y la segunda en descenso o decreciente.
También se puede describir un diagrama de dispersión en coordenadas cartesianas valores como en la distribución diváriate, en donde la nube de puntos representa los pares de valores.
GRAFICOS DE RECTA DE REGRESIÒN:

sábado, 21 de junio de 2008
REGRESION
Según sea la dispersión de los datos (nube de puntos) en el plano cartesiano, pueden darse alguna de las siguientes relaciones, Lineal, Logarítmica, Exponencial, Cuadrática, entre otros.

AJUSTE LINEAL: Y=BX+A
AJUSTE LOGARITMICO: Y=B Ln X+A
AJUSTE EXPONENCIAL: Y=AC BX
AJUSTE PARABOLICO, CUADRATICO O POLINOMIAL: Y= AX2 + BX + A
EstimativosEs una valoracion aproximada basado en datos de periodos anteriores (datos historicos o estadisticos) a traves de muestreos.
PronósticosEs estimar un valor de y dado o supesto un valor de x. Tambien se puede decir que es preveer el futuro.Enuncie Los Pasos Para Ajustar Un Conjunto De Datos Y Crear Un Conjunto Su Modelo MatematicoTener tabulado un conjunto de datos Xi, Yi cuyas variables tengan relación
Utilidades Vs Costos
Costos Vs Cantidad Producida
Utilidades Vs Mes
Costos Vs Semanas
Ingresos Vs Año
Graficar los datos Xi, Yi (Diagrama de dispersion o nube de puntos). Esto permite visualizar la linea de tendencia.Contruya el modelo matematico que mas se ajuste teniendo en cuenta el grado de correlacion.
Perfecta [r]=1
Excelente 0.9 <=[r]<=1 Regular 0.5<=[r]<0.8>tiempo). Algunos ejemplos de series cronológicas serian aspectos tales registros de precipitación pluvial diaria, las ventas semanales, el producto nacional bruto trimestral, mediciones de la temperatura.El objeto de analizar tales datos es determinar si se presentan ciertos patrones o pautas no aleatorias.
basado en datos multidimensionales x,y, donde f es alguna función no lineal respecto a algunos parámetros desconocidos θ. Como mínimo, se pretende obtener los valores de los parámetros asociados con la mejor curva de ajuste (habitualmente, con el método de los mínimos cuadrados). Con el fin de determinar si el modelo es adecuado, puede ser necesario utilizar conceptos de inferencia estadística tales como intervalos de confianza para los parámetros así como pruebas de bondad de ajuste.
El objetivo de la regresión no lineal se puede clarificar al considerar el caso de la regresión polinomial, la cual es mejor no tratar como un caso de regresión no lineal. Cuando la función f toma la forma:
f(x) = ax2 + bx + c
la función f es no lineal en función de x pero lineal en función de los parámetros desconocidos a, b, yc. Este es el sentido del término "lineal" en el contexto de la regresión estadística. Los procedimientos computacionales para la regresión polinomial son procedimientos de regresión lineal (múltiple), en este caso con dos variables predictoras x y x2. Sin embargo, en ocasiones se sugiere que la regresión no lineal es necesaria para ajustar polinomios. Las consecuencias practicas de esta mala interpretación conducen a que un procedimiento de optimización no lineal sea usado cuando en realidad hay una solución disponible en términos de regresión lineal.
El procedimiento mas objetivo para ajustar una recta a un conjunto de datos presentados en
un diagrama de dispersión se conoce como "el método de los mínimos cuadrados". La recta
resultante presenta dos características importantes:
1. Es nula la suma de las desviaciones verticales de los puntos a partir de la recta de ajuste
∑ (Yー - Y) = 0.
2. Es mínima la suma de los cuadrados de dichas desviaciones. Ninguna otra recta daría
una suma menor de las desviaciones elevadas al cuadrado ∑ (Yー - Y)² → 0
(mínima).
El procedimiento consiste entonces en minimizar los residuos al cuadrado:


miércoles, 18 de junio de 2008
jueves, 22 de mayo de 2008
sábado, 10 de mayo de 2008
DIAGRAMA DE CAJAS (BOX PLOT)
AREA BAJO LA CURVA.
La distribución normal, también llamada distribución de Gauss o distribución gaussiana, es la distribución de probabilidad que con más frecuencia aparece en estadística y teoría de probabilidades. Esto se debe a dos razones fundamentalmente:
Su función de densidad es simétrica y con forma de campana, lo que favorece su aplicación como modelo a gran número de variables estadísticas.
Es, además, límite de otras distribuciones y aparece relacionada con multitud de resultados ligados a la teoría de las probabilidades gracias a sus propiedades matemáticas.
La función de densidad está dada por:
Distribución normal estándar. Estandarización [editar]
Cuando y , la distribución se conoce con el nombre de normal estándar.
Dada una variable aleatoria normal X, con media (también llamada Esperanza matemática) y desviación típica , si definimos otra variable aleatoria entonces la variable aleatoria Z tendrá una distribución de porcentaje altamente normal aunque algunas veces muy estándar y a la vez pequeña y . Se dice que se ha tipificado o estandarizado la variable X.
Uso de tablas [editar]
La probabilidad de que una variable aleatoria (que sigue una distribución normal) se encuentre entre dos valores determinados será en general difícil de calcular (hay que usar la integral de la función de probabilidad). Para ello, existen tablas de distribución normal tipificada, si bien éstas se calculan para la distribución Normal Tipificada.
Básicamente, se busca un valor de x (por ejemplo, ), y la tabla nos da la probabilidad de que :
En el caso de que la distribución no sea estándar, por ejemplo, con y , tendremos que tipificar la variable:
Se obtiene una variable Z normal, que además está tipificada. Si ahora se consulta en la tabla,
COMENTARIO.
EL AREA BAJO LA CURVA ES UNA GRAFICA QUE REPRESENTA UNA DISTRIBUCION DE DATOS, EN EL QUE SE ESTUDIA UN PROBLEMA O FENOMENO Y CON EL CUAL SE DETERMINA LA PROBABILIDAD, EL PORCENTAJE Y EL NUMERO DE DATOS QUE SE DESEA SABER O DESCIFRAR, UN RESULTADO ADECUADO O ESPECIFICO SOBRE EL FENOMENO QUE SE ESTE ESTUDIANDO.